前回のDFSプログラムに再帰処理を加えた
はじめに
前回は、2×2の単純なグリッドを開始位置の指定をせずに動いた場合の合計した数値の最大値を出すプログラムを作成した。
今回は、前回のプログラムに再帰処理を加えてみよう。
再帰処理
関数の中で同じ関数を呼ぶこと。
ソースコード
python/dfs.py at 408aeb2a8a5241e15faba038feb5678cf532f993 · ki-hi-ro/python
grid = [
[1, 5],
[0, 9]
]
H, W = len(grid), len(grid[0])
directions = [(1,0), (-1,0), (0,1), (0,-1)]
max_score = 0
best_path = []
def dfs(y, x, visited, total, path):
global max_score, best_path
# 現在の状態を出力
print(f"{path} → 合計={total}")
# 最大値の更新
if total > max_score:
max_score = total
best_path = path[:]
# 4方向へ探索
for dy, dx in directions:
ny, nx = y + dy, x + dx
if 0 <= ny < H and 0 <= nx < W and (ny, nx) not in visited:
dfs(ny, nx, visited | {(ny, nx)}, total + grid[ny][nx], path + [(ny, nx)])
print("=== 再帰的DFSで全パターン探索 ===")
for y in range(H):
for x in range(W):
start_val = grid[y][x]
dfs(y, x, {(y, x)}, start_val, [(y, x)])
print("\n🏆 最大合計:", max_score)
print("通った座標:", best_path)出力結果
=== 再帰的DFSで全パターン探索 ===
[(0, 0)] → 合計=1
[(0, 0), (1, 0)] → 合計=1
[(0, 0), (1, 0), (1, 1)] → 合計=10
[(0, 0), (1, 0), (1, 1), (0, 1)] → 合計=15
[(0, 0), (0, 1)] → 合計=6
[(0, 0), (0, 1), (1, 1)] → 合計=15
[(0, 0), (0, 1), (1, 1), (1, 0)] → 合計=15
[(0, 1)] → 合計=5
[(0, 1), (1, 1)] → 合計=14
[(0, 1), (1, 1), (1, 0)] → 合計=14
[(0, 1), (1, 1), (1, 0), (0, 0)] → 合計=15
[(0, 1), (0, 0)] → 合計=6
[(0, 1), (0, 0), (1, 0)] → 合計=6
[(0, 1), (0, 0), (1, 0), (1, 1)] → 合計=15
[(1, 0)] → 合計=0
[(1, 0), (0, 0)] → 合計=1
[(1, 0), (0, 0), (0, 1)] → 合計=6
[(1, 0), (0, 0), (0, 1), (1, 1)] → 合計=15
[(1, 0), (1, 1)] → 合計=9
[(1, 0), (1, 1), (0, 1)] → 合計=14
[(1, 0), (1, 1), (0, 1), (0, 0)] → 合計=15
[(1, 1)] → 合計=9
[(1, 1), (0, 1)] → 合計=14
[(1, 1), (0, 1), (0, 0)] → 合計=15
[(1, 1), (0, 1), (0, 0), (1, 0)] → 合計=15
[(1, 1), (1, 0)] → 合計=9
[(1, 1), (1, 0), (0, 0)] → 合計=10
[(1, 1), (1, 0), (0, 0), (0, 1)] → 合計=15
🏆 最大合計: 15
通った座標: [(0, 0), (1, 0), (1, 1), (0, 1)]ソースコード全体の解説
グリッドの定義
grid = [
[1, 5],
[0, 9]
]縦と横を取得
H, W = len(grid), len(grid[0])4方向の定義
directions = [(1,0), (-1,0), (0,1), (0,-1)]最大スコアの定義
max_score = 0最大スコアを叩き出した時の経路の定義
best_path = []dfs関数の定義
def dfs(y, x, visited, total, path):
global max_score, best_path
# 現在の状態を出力
print(f"{path} → 合計={total}")
# 最大値の更新
if total > max_score:
max_score = total
best_path = path[:]
# 4方向へ探索
for dy, dx in directions:
ny, nx = y + dy, x + dx
if 0 <= ny < H and 0 <= nx < W and (ny, nx) not in visited:
dfs(ny, nx, visited | {(ny, nx)}, total + grid[ny][nx], path + [(ny, nx)])出力処理
print("=== 再帰的DFSで全パターン探索 ===")
for y in range(H):
for x in range(W):
start_val = grid[y][x]
dfs(y, x, {(y, x)}, start_val, [(y, x)])
print("\n🏆 最大合計:", max_score)
print("通った座標:", best_path)dfs関数の解説
引数には、グリッドの座標y、x、すでに訪れた座標を記録するvisited、合計スコアを計算した結果を格納するtotal、経路を格納するpathが渡される。
def dfs(y, x, visited, total, path):以下のように使用している。
for y in range(H):
for x in range(W):
start_val = grid[y][x]
dfs(y, x, {(y, x)}, start_val, [(y, x)])HとWの値は、以下で定義しているように、2と2。
grid = [
[1, 5],
[0, 9]
]
H, W = len(grid), len(grid[0])これで、第一、二、三、五引数の値が決まる。
def dfs(y, x, visited, total, path):第四引数のtotalには、start_valが入る。
for y in range(H):
for x in range(W):
start_val = grid[y][x]
dfs(y, x, {(y, x)}, start_val, [(y, x)])最初のループ、つまり、(y, x)=(0,0)を見て行こう。

dfs(0, 0, {(0,0)}, 1, [(0,0)])という引数で、dfs関数が実行される。
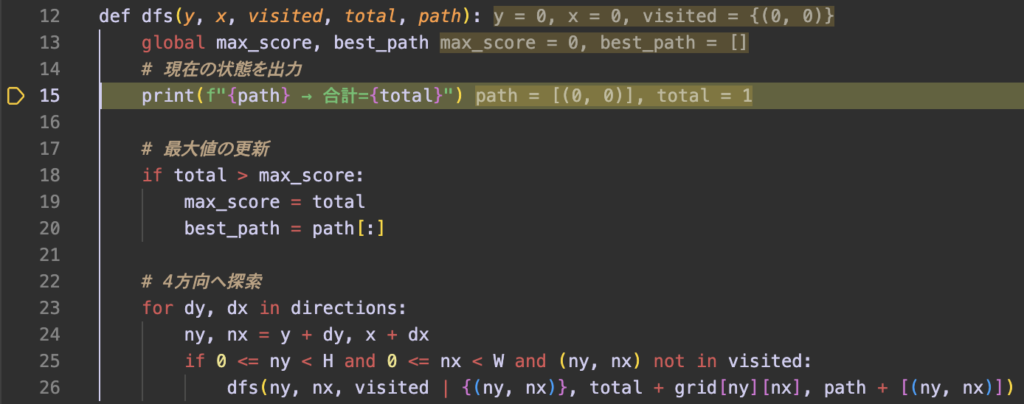
max_scoreとbest_pathは、関数の外側で定義している初期値。
max_score = 0
best_path = []まずは、現在の状態を出力する。
# 現在の状態を出力
print(f"{path} → 合計={total}")(0, 0)の値は、1。
[(0, 0)] → 合計=1次に最大値の更新を行う。
# 最大値の更新
if total > max_score:
max_score = total
best_path = path[:]total=1は、max_score=0よりも大きいので、max_scoreが1になり、best_pathは、(0, 0)になる。
以下の[:]はリストをコピーするという意味。
best_path = path[:]最後に、4方向の探索を行う。
# 4方向へ探索
for dy, dx in directions:
ny, nx = y + dy, x + dx
if 0 <= ny < H and 0 <= nx < W and (ny, nx) not in visited:
dfs(ny, nx, visited | {(ny, nx)}, total + grid[ny][nx], path + [(ny, nx)])
(1, 0)の時、dy, dxは、1, 0になる。
for dy, dx in directions:ny, nxは、y + dy, x + dxなので、0 + 1, 0 + 0、つまり、1, 0になる。
これは、以下の条件に当てはまる。
if 0 <= ny < H and 0 <= nx < W and (ny, nx) not in visited:そのため、以下が実行される。
dfs(ny, nx, visited | {(ny, nx)}, total + grid[ny][nx], path + [(ny, nx)])実際の引数を入れると以下の通り。
dfs(1, 0, {(0,0), (1,0)}, 1 + 0, [(0,0)] + [(1,0)])計算結果は以下。
dfs(1, 0, {(0,0), (1,0)}, 1, [(0,0), (1,0)])これを何回も繰り返した結果、以下の出力になる。
=== 再帰的DFSで全パターン探索 ===
[(0, 0)] → 合計=1
[(0, 0), (1, 0)] → 合計=1
[(0, 0), (1, 0), (1, 1)] → 合計=10
[(0, 0), (1, 0), (1, 1), (0, 1)] → 合計=15
[(0, 0), (0, 1)] → 合計=6
[(0, 0), (0, 1), (1, 1)] → 合計=15
[(0, 0), (0, 1), (1, 1), (1, 0)] → 合計=15
[(0, 1)] → 合計=5
[(0, 1), (1, 1)] → 合計=14
[(0, 1), (1, 1), (1, 0)] → 合計=14
[(0, 1), (1, 1), (1, 0), (0, 0)] → 合計=15
[(0, 1), (0, 0)] → 合計=6
[(0, 1), (0, 0), (1, 0)] → 合計=6
[(0, 1), (0, 0), (1, 0), (1, 1)] → 合計=15
[(1, 0)] → 合計=0
[(1, 0), (0, 0)] → 合計=1
[(1, 0), (0, 0), (0, 1)] → 合計=6
[(1, 0), (0, 0), (0, 1), (1, 1)] → 合計=15
[(1, 0), (1, 1)] → 合計=9
[(1, 0), (1, 1), (0, 1)] → 合計=14
[(1, 0), (1, 1), (0, 1), (0, 0)] → 合計=15
[(1, 1)] → 合計=9
[(1, 1), (0, 1)] → 合計=14
[(1, 1), (0, 1), (0, 0)] → 合計=15
[(1, 1), (0, 1), (0, 0), (1, 0)] → 合計=15
[(1, 1), (1, 0)] → 合計=9
[(1, 1), (1, 0), (0, 0)] → 合計=10
[(1, 1), (1, 0), (0, 0), (0, 1)] → 合計=15
🏆 最大合計: 15
通った座標: [(0, 0), (1, 0), (1, 1), (0, 1)]深さについて
出力結果を見てもらえれば分かるが、ダイバーのように深く潜っている。
(y,x)が(0,0)の時を見ていこう。
[(0, 0)] → 合計=1
[(0, 0), (1, 0)] → 合計=1
[(0, 0), (1, 0), (1, 1)] → 合計=10
[(0, 0), (1, 0), (1, 1), (0, 1)] → 合計=15
[(0, 0), (0, 1)] → 合計=6
[(0, 0), (0, 1), (1, 1)] → 合計=15
[(0, 0), (0, 1), (1, 1), (1, 0)] → 合計=15以下のグリッド上のお話。
grid = [
[1, 5],
[0, 9]
]以下の条件(次の座標がグリッド上にある、すでに訪れていない)に当てはまれば、進むことができる。
if 0 <= ny < H and 0 <= nx < W and (ny, nx) not in visited:
第三引数のvisited | {(ny,nx)}は、和集合。
集合同士の和集合演算を行なっている。
{(0,0)}と{(1,0)}の和集合は、{(0,0), (1,0)}になる。
グリッド上の値を拾っていくと以下のようになる。
[(0, 0)] → 合計=1・・・1
[(0, 0), (1, 0)] → 合計=1・・・1→0
[(0, 0), (1, 0), (1, 1)] → 合計=10・・・1→0→9
[(0, 0), (1, 0), (1, 1), (0, 1)] → 合計=15・・・1→0→9→5
[(0, 0), (0, 1)] → 合計=6・・・1→5
[(0, 0), (0, 1), (1, 1)] → 合計=15・・・1→5→9
[(0, 0), (0, 1), (1, 1), (1, 0)] → 合計=15・・・1→5→9→0一歩進む、さらに一歩進む・・・というように(0,0)が始点で考えられる最大の探索を行う。
行きと帰り
再帰処理には、行きと帰りという概念がある。
dfs関数の中でdfs関数が呼ばれた時、以下のように新しいスタックが追加される。
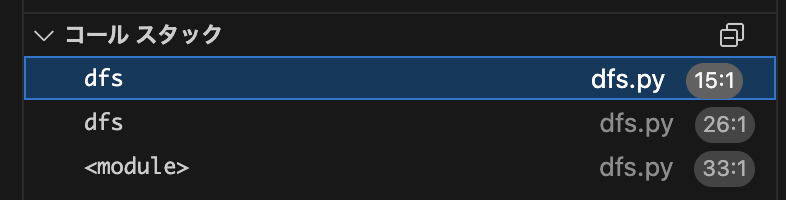
以下が一番深いところ。
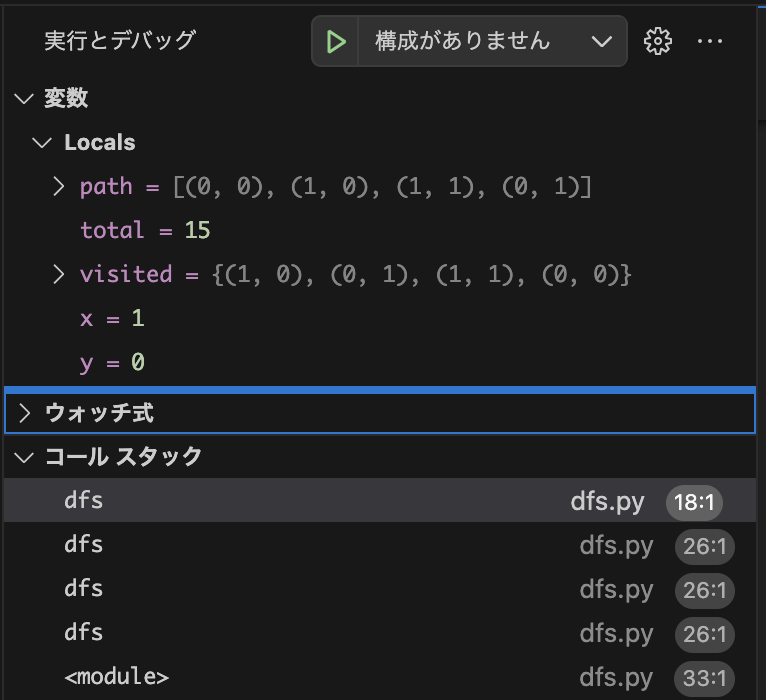
ここから引き返していく。
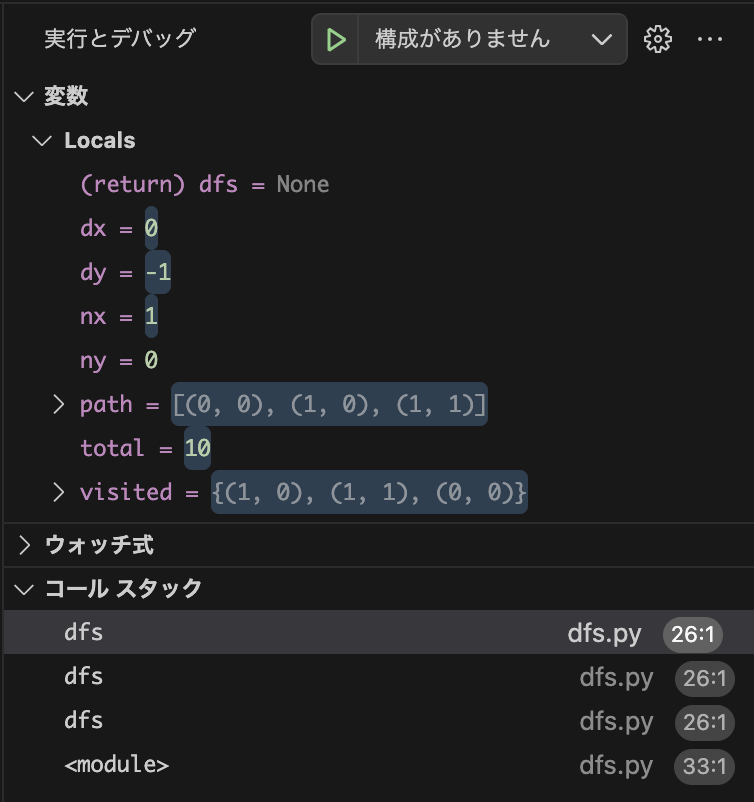
コールスタックが徐々に減っていくところに注目していただきたい。
もうこれ以上移動できないから、スタックが削除される。
5まで行くと、左も下もすでに通っている(visited)ことになる。

9時点のdfs、0時点のdfsも同様に、調べ尽くした状態となる。
1まで戻った。
4方向調べると、右方向(dy=0、dx=1)に進めるようだった。

[(0, 0), (0, 1)] → 合計=6合計は6で、これまでの最大値15よりも小さいので、max_scoreとbest_pathの更新は行われない。
# 最大値の更新
if total > max_score:
max_score = total
best_path = path[:]下方向(1, 1)に進めた。
[(0, 0), (0, 1), (1, 1)] → 合計=15(1, 1)から左方向(0,1)に進めた。
[(0, 0), (0, 1), (1, 1), (1, 0)] → 合計=15ここから下り坂に突入する。
コール スタックのdfsの数が減っていく。
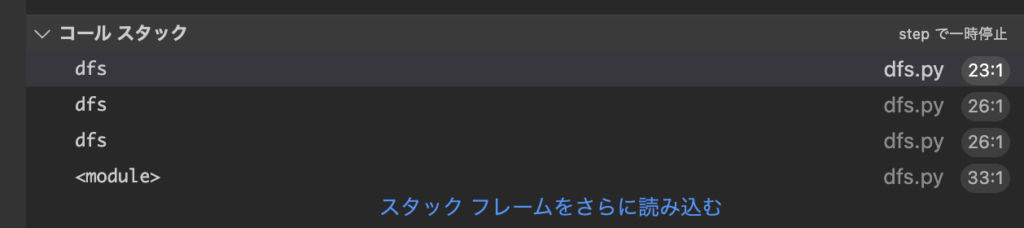
ここは理解しにくいが、以下の部分で4方向のどれも行けずに、再帰処理が終了していることが分かった。
# 4方向へ探索
for dy, dx in directions:
ny, nx = y + dy, x + dx
if 0 <= ny < H and 0 <= nx < W and (ny, nx) not in visited:
dfs(ny, nx, visited | {(ny, nx)}, total + grid[ny][nx], path + [(ny, nx)])
コメントを残す