幅優先探索で最短経路を求める

前回は、プレーンな幅優先探索を行なった。

幅優先探索をマスターする

今回やりたいのは、最短経路探索。

ブラックボックスをいかに使いこなすか

人体の仕組みをはじめとして、ブラックボックスになっていることは多い。

その中身を知ろうとすると、膨大な時間がかかる。

プログラミングにおける関数も中身を知らなくても、入力（引数）と出力（戻り値）だけ意識すれば、うまく組み合わせることで、プログラムを作成していける。

最短経路検索の関数

from collections import deque

def bfs_shortest_path(graph, start, goal):
    queue = deque([[start]])  # キューに「経路のリスト」を入れる
    visited = set()           # 訪問済みノード

    while queue:
        path = queue.popleft()  # 現在の経路
        node = path[-1]         # 現在のノード

        if node == goal:
            return path  # 最短経路が見つかった！

        if node not in visited:
            visited.add(node)
            for neighbor in graph[node]:
                new_path = path + [neighbor]  # 新しい経路を作成
                queue.append(new_path)

    return None  # 経路が見つからなかった場合

# 使用例
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

start_node = 'A'
goal_node = 'F'
shortest_path = bfs_shortest_path(graph, start_node, goal_node)

print("最短経路:", shortest_path)

実行結果

最短経路: ['A', 'C', 'F']

グラフのイメージ

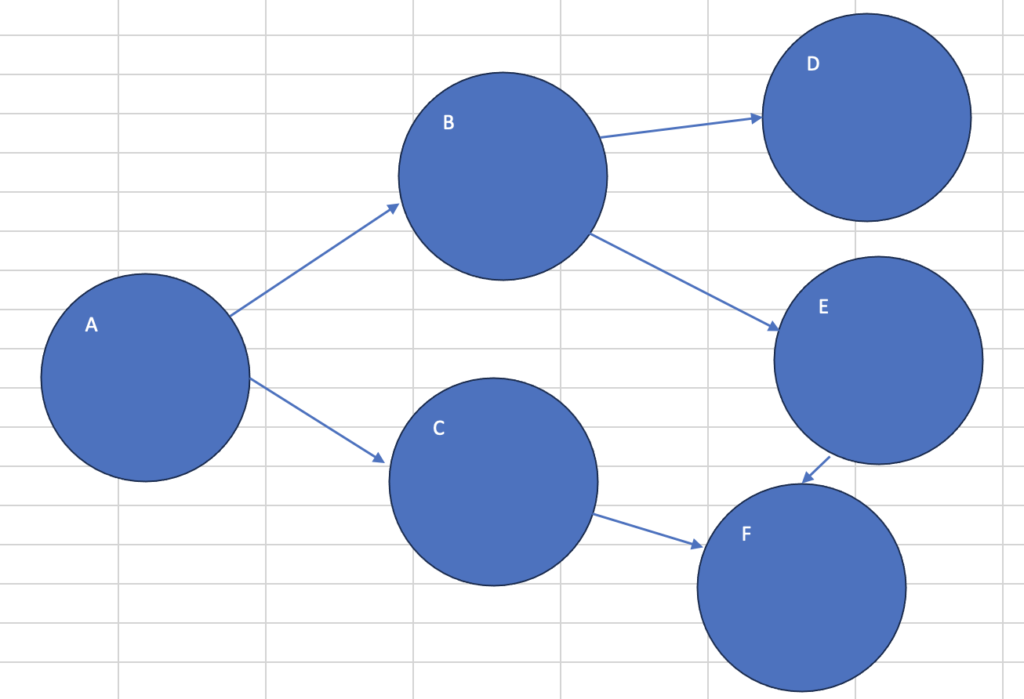
Aがスタート、Fがゴール

最短経路は、A→C→F。

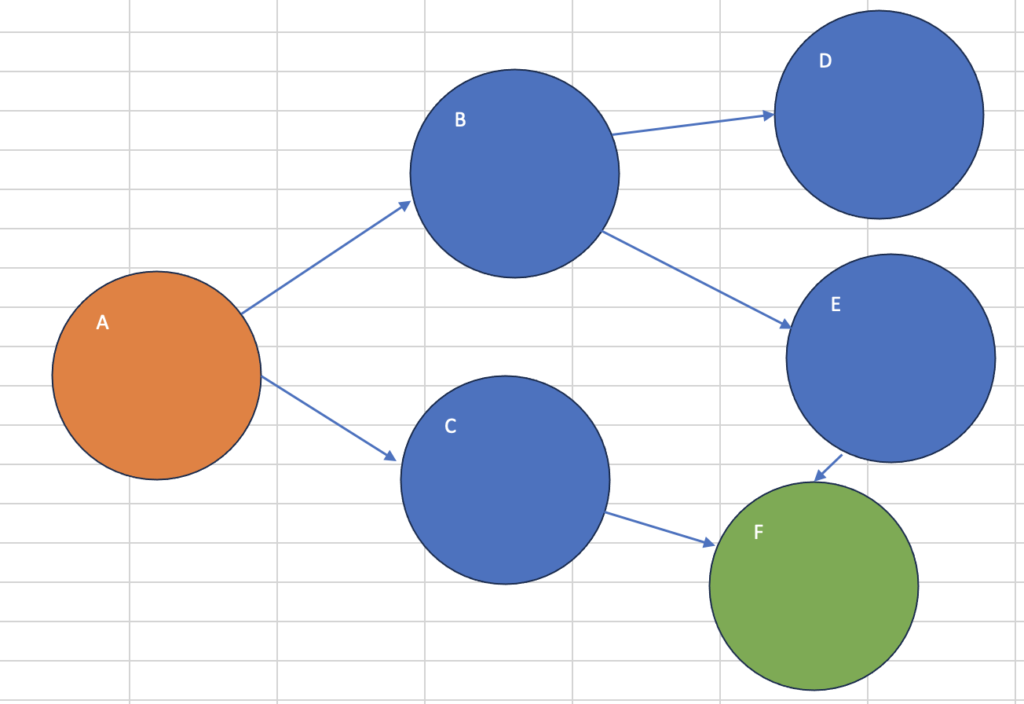
Aがスタート、Eがゴール

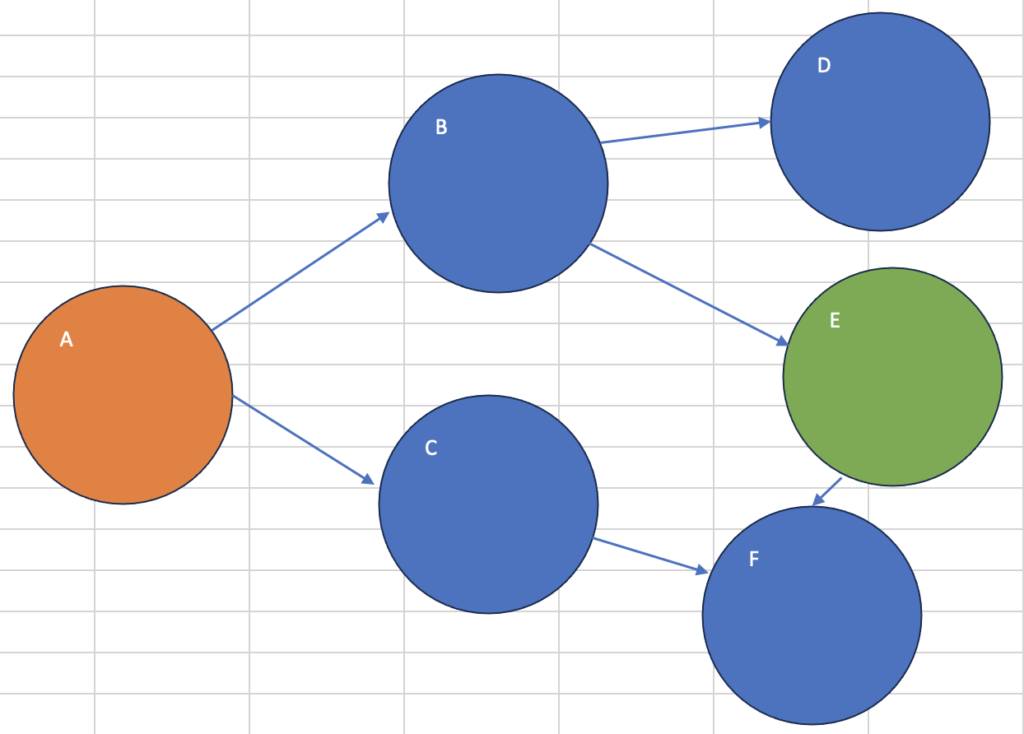
start_node = 'A'
goal_node = 'E'
shortest_path = bfs_shortest_path(graph, start_node, goal_node)

print("最短経路:", shortest_path)

最短経路: ['A', 'B', 'E']

Cがスタート、Bがゴール（異常系）

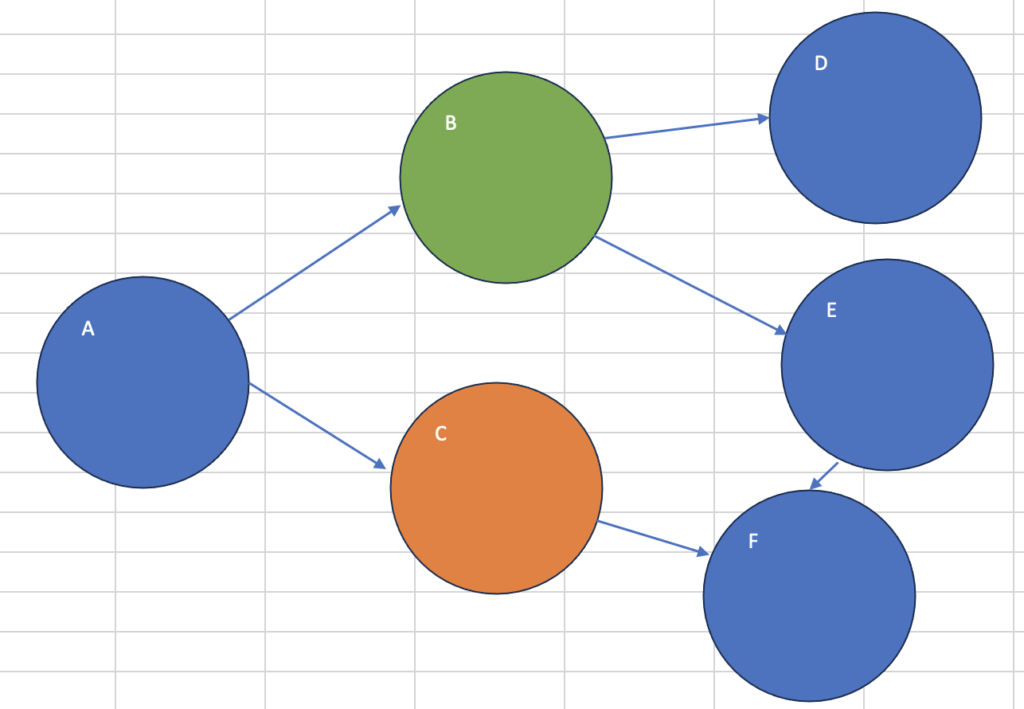
start_node = 'C'
goal_node = 'B'
shortest_path = bfs_shortest_path(graph, start_node, goal_node)

print("最短経路:", shortest_path)

最短経路: None