1/3を計算すると0.333333・・・だが、1/3+1/3+1/3が1になる理由
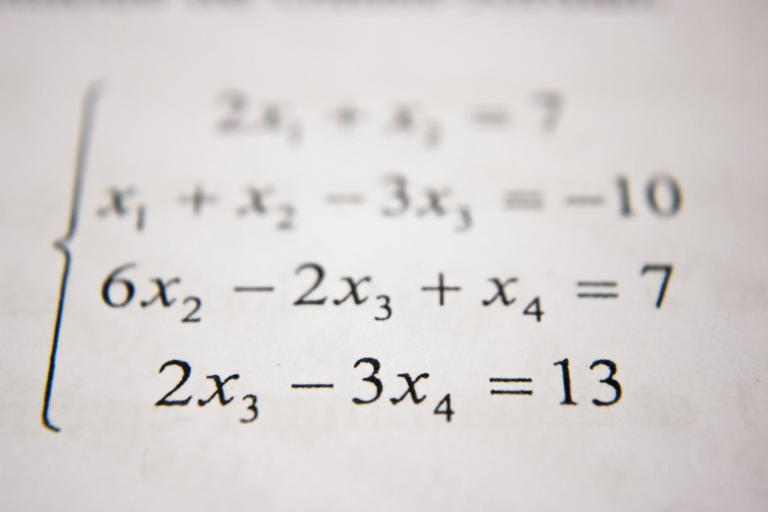
はじめに
昨日、電車の中でタイトルにあるように「1/3は0.33333・・・なのに、1/3+1/3+1/3は1になる」という謎について話している人がいました。
言われてみると確かに不思議です。
1/3が0.33333・・・ならば、1/3+1/3+1/3は0.9999999・・・になるはずです(厳密に言えば)
その謎を数学の知識を用いて説明していきます。
循環小数
1/3+1/3+1/3=0.999999・・・の右辺は、9が無限に続く循環小数です。
無限等比数列
0.9999999・・・は、「0.9 + 0.09 + 0.009 + 0.0009 + ・・・」と表すことが出来ます。
これは、0.9が初項、0.1が公比の等比数列であり、無限に続くので「無限等比数列」と呼ばれます。
1に収束する
無限等比数列では、以下のことが成り立つことが証明されています。
-1<公比<1のとき、「初項 /(1 - 公比)」に収束する「0.9 + 0.09 + 0.009 + 0.0009 + ・・・」は、「0.9 /(1 – 0.1)」に収束します。
0.9 / 0.9 = 1なので、1に収束するということです。
直観的に考えても、0.999999・・・は、1に限りなく近づくことが理解できます。
例えば、0.99999999999999999999999999999は、ほとんど1ですよね。
1/3 = 0.3333・・・は1/3に収束する
先程の公式を1/3にも当てはめてみます。
1/3 = 0.3333・・・は、「0.3 + 0.03 + 0.003 + 0.0003・・・」と表すことが出来ます。
初項0.3、公比0.1の無限等比級数です。
公比0.1は、-1<公比<1という条件に当てはまります。
初項 /(1 – 公比)に当てはめると、0.3 /(1 – 0.1)= 1/3となります。
発散と収束
入門『地頭力を鍛える』 32のキーワードで学ぶ思考法で、発散と収束というキーワードについて解説されています。
会議などでアイディアを自由に話して発想を広げていくのが「発散」です。
会議後にアクションプランとして、やるべきタスクを絞っていくのが「収束」です。
自分の人生でやるべきことを絞り込む時にも、まずは自由にやりたいことのイメージを膨らませてみて(発散)、具体的なやるべきことに落とし込んでいく(収束)のがいいのではないでしょうか。
参考にしたサイト
以下のサイトを参考にしました。
サイエンスナビゲーターの桜井さんが分かりやすく解説してくれています。

コメントを残す