基本情報技術者 令和元年 秋期 午前の過去問を解いてみた①

はじめに
こちらのサイトから基本情報技術者試験の過去問を見ることができます。
今回、令和元年秋期の過去問を解いてみました。
第一回目は、問1~問10です。
問1
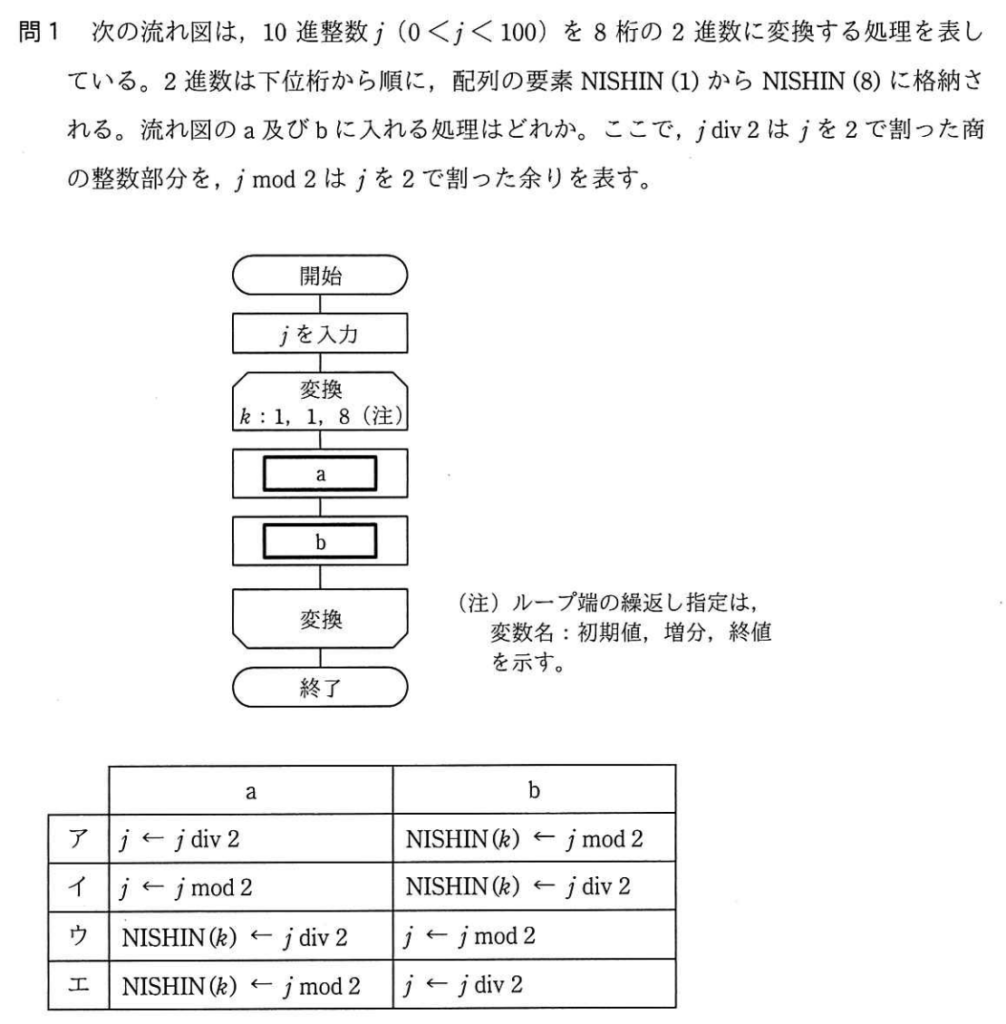
10進整数j(0 < j < 100)の条件に当てはまる「4」という数字で考えてみる。
流れ図の「jを入力」で、j = 4となる。
次のループで、繰り返し処理が始まる。
一般的に、10進数を2進数に変換するときは、商が0になるまで2で割っていき、余りを反対方向に並べるという流れをたどる。
4の場合、商が0になるまで2で割っていくと以下のようになる。
- 4 ÷ 2 = 2・・・0
- 2 ÷ 2 = 1・・・0
- 1 ÷ 2 = 0・・・1
そして、余りを反対方向に並べると100になる。
問題文では、aという処理の後にbが来ている。
繰り返しの中で最初に行うのは、商を2で割った時の余りを取り出すことなので、
aには、NISHIN(k) ← j mod 2 が入る。
次に、最初の計算結果の商を次の計算に利用するという流れとなるので、
bには、j ← div2 が入る。
よって、エが正解。
問2

適当な8ビットの値「10101010」を用意して考える。
選択肢で、16進数表記は00かFFの2パターンある。
論理演算は、排他的論理和か論理和の2パターンある。
まずは、16進数表記を2進数に変換する。
以下の対応表を参考にする。
| 10進数 | 2進数 | 16進数 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 10000 | 10 |
00は、00000000
FFは、11111111と考えることができる。
確認すべきパターンは以下の4つとなる。
- 10101010 と 00000000 の排他的論理和・・・ア
- 10101010 と 00000000 の論理和・・・イ
- 10101010 と 11111111 の排他的論理和・・・ウ
- 10101010 と 11111111 の論理和・・・エ
排他的論理和のベン図と真理値表は以下の通り。
ベン図
真理値表
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
論理和
ベン図
真理値表
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
アの場合、0 + 0 = 1で反転するが、1 + 0 = 1で反転しないので、誤り。
イの場合、0 + 0 = 0、1 + 0 = 1となり、反転しないので、誤り。
ウの場合、0 + 1 = 1、1 + 1 = 0となり、全てのケースで反転するので、ウが正解。
エの場合、0 + 1 = 1で反転するが、1 + 1 = 1で反転しないので、誤り。
問3
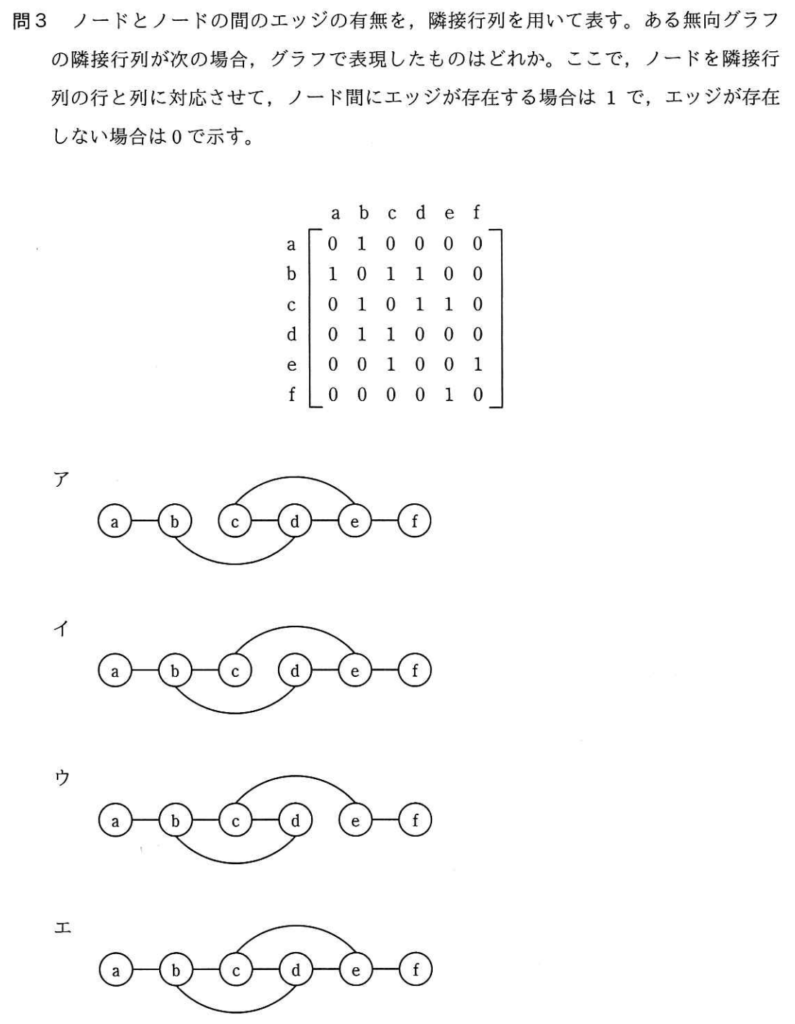
アは、bとcが繋がっていないが、隣接行列ではc列b行が1なので、誤り。
イは、cとdが繋がっていないが、隣接行列ではc列d行が1なので、誤り。
ウとエの違いは、dとeが繋がっているかどうかということ。
隣接行列を見ると、e列d行、d列e行が0なので、dとeは繋がっていない。
よって、dとeが繋がっていない「ウ」が正解。
問4
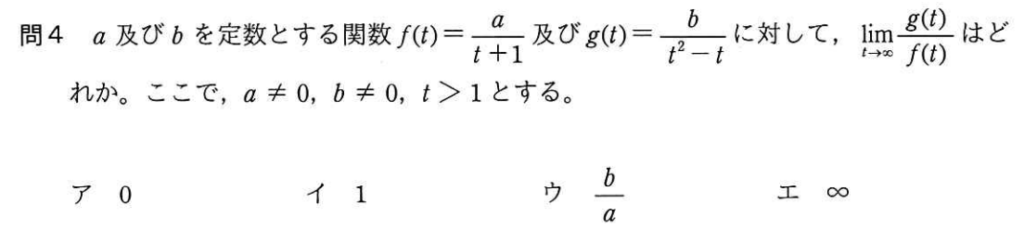
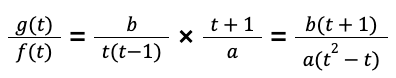
分母・分子を、
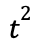
で割ると、


問5
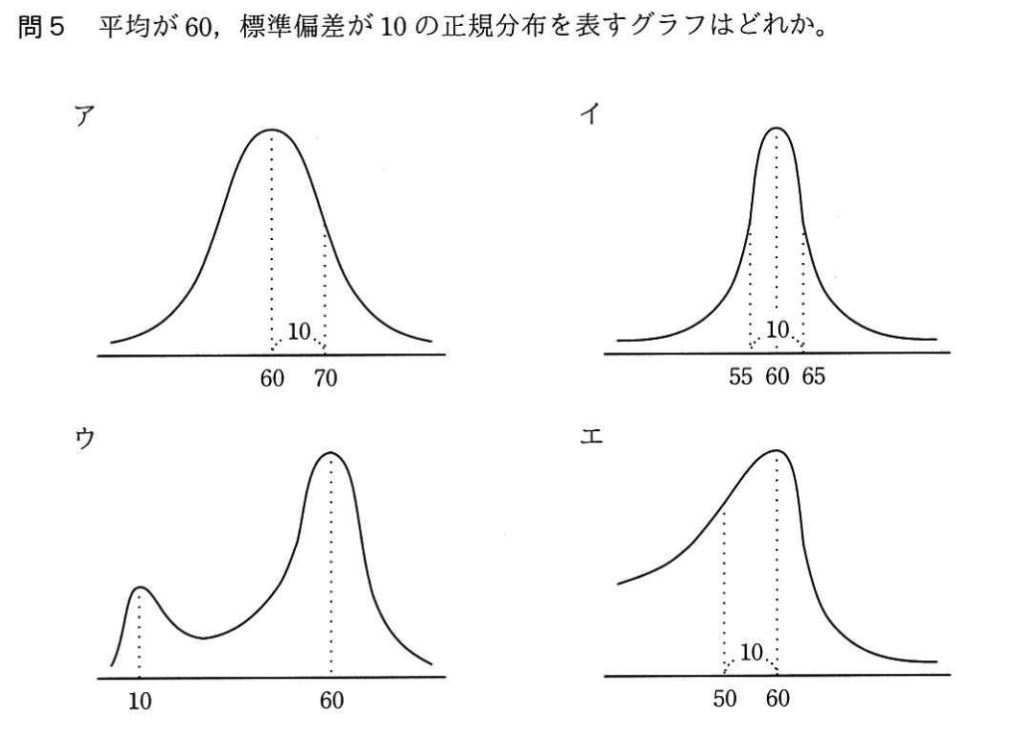
標準偏差のグラフは、平均が真ん中に来る。
よって、ウとエは不正解。
標準偏差は、データが平均点の周辺でどれくらいばらついているかを表す。
標準偏差が10の場合、平均から10だけ離れたところにデータがある。
よって、アが正解。
問6

例えば、nが10の時を考える。
Cの値が0になるのは、AとBが同じ数字になった時。
AとBが同じ数字になるのは、0, 1, 2・・・9の10通り。
Cの値として考えられるのは、10 × 10 = 100通り。
よって、Cの値が0になる確率は、10 ÷ 100 = 1/10。
よって、ウが正解。
問7

変数名には、「英字」か「変数名 + 英数字」が入る。
最初に「_」や数字が来ることはないので、エが正解。
問8

スタックを3つ用意する必要がある。
例えば、一つ目のスタックに、A→Sの順に文字を入力する。
二つ目のスタックに、C→Tの順に文字を入力する。
三つ目のスタックに、Kを入力する。
取り出すときは、スタックなので、後に入れたものから取り出す。
一つ目からSを、二つ目からTを、一つ目からAを、二つ目からCを、三つ目からKを取り出すと、STACKという文字列が完成する。
よって、ウが正解。
問9
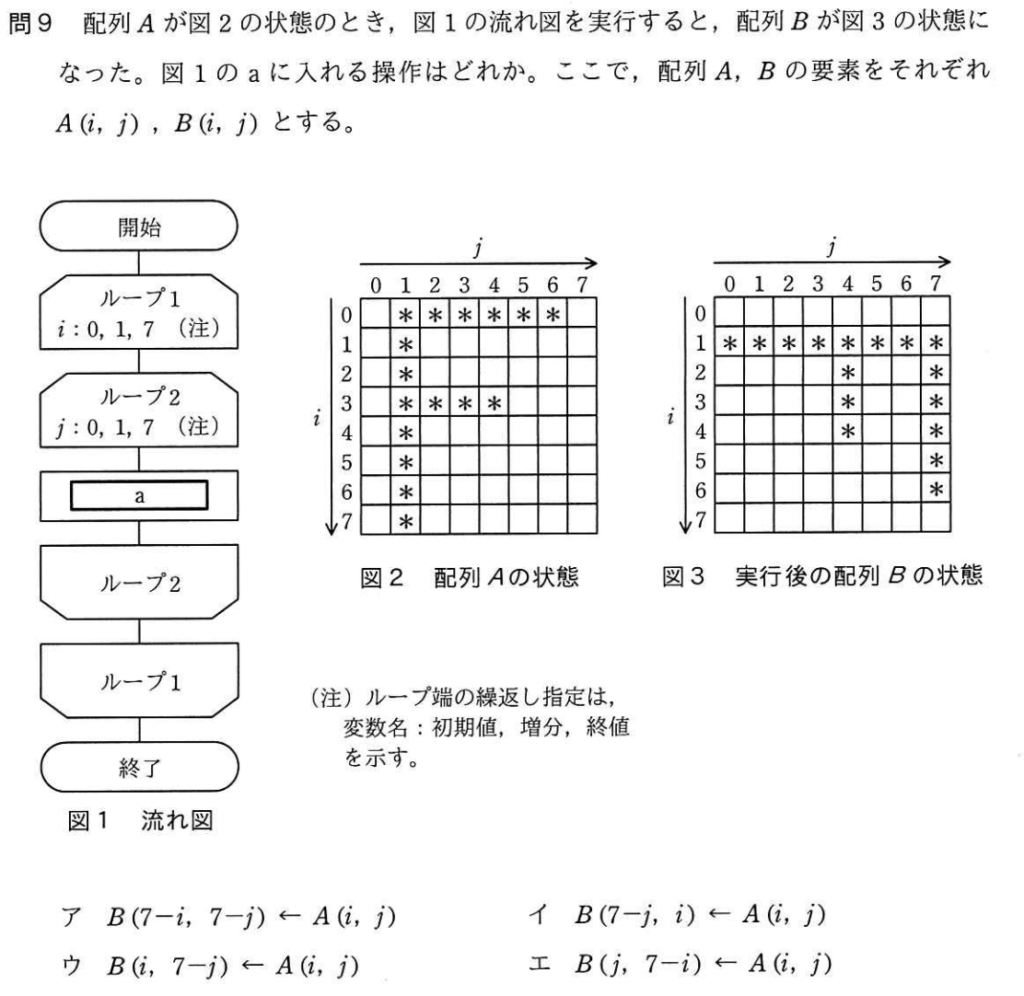
(j,i)が(1,0)の時を考える。
ア〜エの処理で、iとjの順番がそれぞれ違うことに注意する。
アの処理を行うと、(i,j)が(7,6)となり、図3を見るとマークがついていないので、アは誤り。
イの処理を行うと、(j,i)が(6,0)となり、図3を見るとマークがついていないので、イは誤り。
ウの処理を行うと、(i,j)が(0,6)となり、図3を見るとマークがついていないので、ウは誤り。
エの処理を行うと、(j,i)が(1,7)となり、図3を見るとマークがついているので、エが正解。
問10

54321に対して、a1+a2+a3+a4+a5を行うと、15になる。
mod(15, 13)は、2になる。
よって、54321は2の位置に入る。
イが正解。

コメントを残す